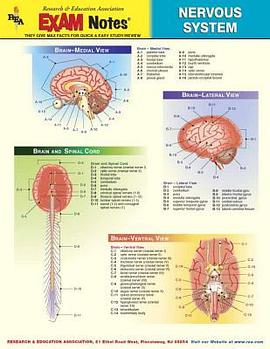
具体描述
EXAM Notes "RM" are double-sided, laminated charts that contain all the information students need on one single chart. They are colorful and exceptionally well-organized to simplify and speed study. The most often used and required facts and formulas are included. EXAM Notes function as study tools, homework aids, and for reference at work. This series of charts covers a great variety of subjects, including anatomy, business/accounting, computer programming, grammar/writing, U.S. & European history, languages, math, physical & social sciences.
作者简介
目录信息
读后感
评分
评分
评分
评分
用户评价
这本书简直是为我这种数学恐惧者量身定做的!我一直对代数抱有一种敬而远之的态度,总觉得那些字母和符号是某种神秘的咒语,让人望而生畏。然而,当我翻开《Exam Notes Introductory Algebra St》时,那种焦虑感奇迹般地消散了。作者的叙述方式极其平易近人,仿佛一位经验丰富的导师坐在你身边,用最生活化的语言解释那些抽象的概念。比如,讲解方程的解时,它没有直接抛出复杂的公式,而是用“天平原理”进行了生动的比喻,让我瞬间明白了保持等式平衡的精髓。更让我印象深刻的是,它对基础概念的夯实工作做得非常到位。很多其他教材一笔带过的内容,比如有理数运算的优先级、负数的乘法法则,这本书都进行了详尽的分解和大量的实例支撑。我特别喜欢它在每一章末尾设置的“常见误区解析”部分,精准地指出了初学者最容易犯错的地方,并提供了纠正的方法。这不仅仅是一本考试复习资料,更像是一本可以陪伴你从零开始建立代数思维的工具书。我感觉自己不再是被动地记忆规则,而是真正理解了代数这门语言的逻辑和美感。对于那些准备参加基础代数考试,又担心基础不牢固的朋友来说,这本书的价值无可估量。它不是那种堆砌难点试图炫耀难度的书籍,而是真正致力于让每一个读者都能跨越入门的门槛,稳健前行。
评分我是一位在职人士,学习时间非常碎片化,所以对于任何学习材料的“可携带性”和“即时性”要求极高。这本书的物理设计——如果把它放在实体的角度来看——简直是教科书式的完美。它的开本适中,便于单手翻阅,纸张的质量也很好,即使用荧光笔做了大量标记,也不会透墨。但这只是外在的优点,其真正的价值在于其内容的**模块化设计**。每一个知识点都被切割成易于消化的“小卡片”单元。如果我只有十分钟的空闲时间,我可以迅速翻到某个特定的公式回顾,而不需要浏览一大段文字。它对于复习特定的知识点,如二次方程的求根公式的应用限制,提供了即时且精准的反馈。此外,书中对“重难点”的标记非常直观,通常会用不同颜色的字体或边框来区分“必考点”和“选修拓展”,这帮助我能够根据自己的应试需求,高效地分配学习精力。对于时间紧张的学习者来说,这本书提供的不是知识的海洋,而是一张精心绘制的、直达目标的小径地图,省去了自己筛选信息的巨大成本。
评分这本书的“笔记”性质体现得淋漓尽致,但其深度却远超我预期的简单速查手册。我过去使用的某些复习材料,通常只告诉你“怎么做”,但很少告诉你“为什么这么做”。《Exam Notes Introductory Algebra St》则在这方面做得非常出色。它不是简单地罗列定理,而是在关键的证明步骤中,插入了作者的个人洞察和历史背景。例如,在讲解因式分解时,它穿插了对完全平方公式和平方差公式历史演变的小段描述,这让原本枯燥的代数公式有了一种“生命感”。更重要的是,它对代数符号系统的**一致性**维护得非常好,从头到尾都确保了变量、系数和运算符的表示法是统一且清晰的,避免了不同章节之间因为符号使用习惯不同而产生的混淆。对于一个需要长期、系统性学习代数概念的读者来说,这种高度的专业性和一致性是保证学习质量的关键。我甚至发现,即便是那些我自认为已经掌握的部分,通过作者的重新阐述,也挖掘出了更深层次的理解。它教会我的不仅仅是解题技巧,更是一种严谨的数学思维方式。
评分老实说,我拿到这本书时,内心是抱持着一丝怀疑的。市面上关于基础代数的“Notes”太多了,很多都只是把教科书的知识点生硬地罗列出来,重点不突出,重点是公式和定义就是一堆冰冷的文字,读起来像是在啃干涩的木头。然而,这本书在排版和内容组织上的用心程度,绝对是教科书级别的体验。它的结构设计非常巧妙,章节之间的逻辑递进是自然而然的,很少出现突然跳跃到下一个高级概念的情况。我特别欣赏它在引入新知识点时所采用的“循序渐进,案例驱动”的方法。比如,在讲解函数图像的平移和拉伸时,它没有直接给出$f(x-h)$和$a cdot f(x)$的公式,而是先展示了一系列不同参数下图像的实际变化动画(当然,在书本上是通过精妙的图示来模拟的),让读者先“看”到现象,再去理解背后的数学原理,这种由观察到归纳的学习路径,极大地降低了理解的门槛。而且,本书的例题选择既有基础巩固型的,也有略带挑战性的应用题,真正能帮助读者检验自己是否掌握了该章节的核心技能。对于需要高效备考的人来说,这种精炼而不失深度的内容组织是极其高效的学习资源。
评分作为一名对数学学习方法有较高追求的读者,我越来越发现,学习代数不仅仅是解题,更是对逻辑推理能力的训练。这本书在培养这种能力方面,展现出了超越基础教材的洞察力。它不仅仅是“教你怎么算”,更侧重于“教你如何思考一个代数问题”。例如,在处理不等式这类需要考虑区间和边界条件的问题时,它详细展示了如何通过**可视化**(尽管是以文字和图示结合的形式)来构建思维模型,避免在解题过程中忽略了关键的界限条件。我尤其欣赏它在引入某些更高级的代数技巧(例如配方法在处理最大值/最小值问题中的应用)时,所体现出的**优雅性**。它没有把这些技巧包装成必须死记硬背的捷径,而是将其置于一个更广阔的数学背景下进行阐述,让读者感受到这些工具的强大和通用性。这本书成功地将严谨的学术要求与高效的学习实践完美地结合在了一起,它让我觉得,代数不是一门令人沮丧的科目,而是一门充满发现和逻辑美感的艺术。它为我未来的深入学习打下了一个非常坚实且充满信心的基础。
评分 评分 评分 评分 评分相关图书
本站所有内容均为互联网搜索引擎提供的公开搜索信息,本站不存储任何数据与内容,任何内容与数据均与本站无关,如有需要请联系相关搜索引擎包括但不限于百度,google,bing,sogou 等
© 2026 book.quotespace.org All Rights Reserved. 小美书屋 版权所有